My last article, pre-Santa Claus, was about the Moon. One of the things I mentioned was that the Moon is responsible for the tides, so let’s talk about that. It’s a good opportunity to talk about some useful Physics
First off, let’s clarify that the Moon isn’t the only thing that influences the tides, it’s just the main one. The gravitational force of the Sun also plays a role, as does the centrifugal force generated by the rotation of the Earth. Now is also probably a good time to talk about the concept of “force”, as far as Physics is concerned. We’ve already talked about gravity and bricks falling down and all that, in the articles about energy. So, “the force of gravity” is something we’re all familiar with, but only as a concept.
In Physics terms, a force is defined as a mass (any object) undergoing acceleration. We tend to think of acceleration as is applies to the gas pedal (accelerator) in a car, so we can work with that. We generally think acceleration means “to go faster”, but that’s not necessarily the case. Your car actually has two accelerators. The other is the brake pedal, which causes a “negative acceleration”, which slows you down. Acceleration is what is called a “vector quantity”. Don’t panic. A vector just means that it has both a magnitude (how fast you are speeding up or slowing down) and a direction. If you are in your car, pointed in a straight line, and you push on the gas, you are accelerating forward. If you push on the brake, the acceleration is backward.
Since the definition of force is a mass undergoing acceleration, it is easy to calculate (in a simple case like this) as mass (m) X acceleration (a). Say your car has a mass of 1000 kilograms (kg, all sciences use the metric system, because the standard system is uniformly stupid and much harder to use) which is about 2200 pounds (it’s a small car). Let’s further say that you are traveling at a constant speed of 10 meters (m) per second, which is equivalent to about 22 mph. If you are traveling at a constant speed, you aren’t accelerating, so the force on the car is 0 (2000kg X 0m/sec2=0, m X a =0). In reality, there are all sorts of forces acting on your car, like friction and wind resistance, which is why you are still burning gas even when you are driving at a constant speed, but let’s not complicate things. Let’s say you decide to speed up. If you start with a velocity of 10 m/sec and you want to speed up to 20 m/sec over the course of 10 seconds, your acceleration is 10m/sec/sec or “1 meter per second per second” or more properly, 1 m/sec2, spoken as 1 “meter per second squared”. Don’t get too freaked out over all that. It’s easy to understand when you are going 10 m/s. Velocity is a distance over time, meters per second, mile per hour, furlongs per fortnight, or whatever other units you choose to use. Simple. Acceleration is just changing that velocity over a period of time, so acceleration becomes meters per second per second. So, if you are in your 1000 kg car, accelerating at 10 m/s2 the force on the car is 10000 kg x m/sec2. Since “kilogram-meter per second squared” is awkward to say and gets said a lot in Physics, that unit has been renamed “the Newton”, after Sir Isaac. 1 Newton of force is equivalent to 1 kg x m/sec2. When you are accelerating in your car as above, you push on the gas to increase the power of the engine and the engine exerts a force of 10,000 N on your car, and since force has both a magnitude (10,000N) and direction, it’s important to remember that it is accelerating forward, increasing the velocity, so the force is positive. If you hit the brakes and go from 110m/s back to 100 m/s, the acceleration is now negative or -10m/s2 and the force on the car is now negative or -10,000N.
Let’s translate that to the force of gravity. We’ve talked before about how gravity is a property of mass, meaning any two objects with mass will exert an attractive force on one another, like the Earth does on us. Remember that, not only does the Earth exert gravity on us, we also exert gravitational attraction on the Earth. If we jump off a table, we pull the Earth upward just as hard as the Earth pulls us down. However, since the Earth has WAY more mass than a person, and, thus, WAY more inertia, the Earth doesn’t rise up to meet us—we fall to meet it. How fast we (or anything else) falls toward the Earth is a constant, called the gravitational constant, or G, for short. The acceleration due to gravity (G) on Earth is 9.8 m/s2. That means that when you fall, after one second, you are falling at 9.8 m/s. After 2 seconds, you are moving at 19.6 m/s and so on. If you were falling in a vacuum, you would continue to accelerate at 9.8 m/s2 until you hit the ground. However, due to air resistance, you will reach what is called “terminal velocity”, where the wind resistance pushing against you equals the gravitational force pulling you down, and you will stop speeding up. For a human, this is about 53 m/s (120 mph). In case you were wondering, a person would have to fall about 1500 feet to reach terminal velocity.
So, here’s where we bring all this back to the tides. The Moon and the Sun both exert gravitational force on the Earth, including the oceans, so it’s fairly easy to understand how that could affect tides. However, as I mentioned in the beginning, there is also the “centrifugal force” generated by the Earth’s rotation. I put “centrifugal force” in quotes because, despite the fact that we all know what it means, it’s not a real force. What we perceive as “centrifugal force” is actually based on what we experience from our frame of reference. The actual force is called centripetal force, and it is directed toward the center of the circle, not outward, as we perceive “centrifugal force” to do. Let me explain.
Remember Newton’s First Law of Motion? Any object in motion will tend to continue moving in a straight line unless some force acts upon it. That means that a ball rolling across a surface would continue rolling in the same direction at the same velocity forever, unless something changes it. In reality, that ball would eventually stop, due to friction, which is a force acting upon it. Let’s say you tie a string to the ball and start to swing it around in a circle. The ball still “wants” to move in a straight line, but the string is constantly pulling on it, making it move in a circle. The force generated by the string pulling on the ball is the centripetal force, which is always directed toward the center of the circle (you, in this case). But as we all know, if we let go of the ball, it will fly away from the circle, right? That’s what we perceive as “centrifugal force”. The thing is, however, that our perception is wrong. The ball doesn’t fly away from the center of the circle. It will just continue going straight from whatever point we released it. There are lots of good internet videos to help explain this.
That sounds complicated, but it’s really not that bad. When you were a kid, you probably put some water in a bucket, then slung the bucket around in a circle over your head and were amazed that the water stayed in the bucket. The easiest explanation was because the “centrifugal force” acting to keep the water in the bottom of the bucket as you slung it around in the circle was greater than the force of gravity acting to pull the water out of the bucket when it was upside down. Similarly, you feel the effect every time you go around a curve in your car. When you turn to the left, for instance, your body (and your car) seems to want to slide to the right. The faster you go around the turn, the more your body wants to move. If you go around the turn too fast, the force acting on your car will exceed the friction between your tires and the road (gravity is pulling your car down against the road and the tires generate friction against the road) and your car will slide into the ditch. The thing is that your perception of the situation isn’t what is actually happening. The water stays in the bucket because of its inertia. The bottom of the bucket is pushing against the water. Your arm is holding the bucket. It’s your arm that is providing the centripetal force to keep the bucket moving in a circle, and the bucket is keeping the water in place. If you slow the velocity that you swing the bucket, eventually, both the water and the bucket will stop going in a circle and the water will fall out, followed by the bucket, due to gravity. In the car scenario, your car (and you) doesn’t actually want to slide to the right. What it wants to do is go straight and your turning the wheels to the left is keeping it from doing that. What you feel as the tendency to slide to the right is just because the car is turning to the left underneath you.
The Earth rotates really fast. As you are sitting there at your kitchen table with your coffee, you are actually moving about 1000 miles per hour (1600 km/h). That calculation is made based on the circumference of the Earth being about 25,000 miles (40,000 km) and the time necessary for one rotation, which is 24 hours. 25,000 miles divided by 24 hours is about 1040 miles/hr.
Anything that is spinning (going along a curved path) will generate centripetal force. The Earth is no exception. The rotational speed of the Earth causes everything to want to fly off into space, while gravity holds it down to the surface. The Earth is actually a little bigger around the equator than it is if you measure it around the poles because the centripetal force of its rotation causes it to “bulge” a little around the equator. That same force acts on the water in the oceans, as does the gravitational pull of the Moon. There are lots of good images of this on the internet, if you would like a visual to help you. Try https://scijinks.gov/tides/
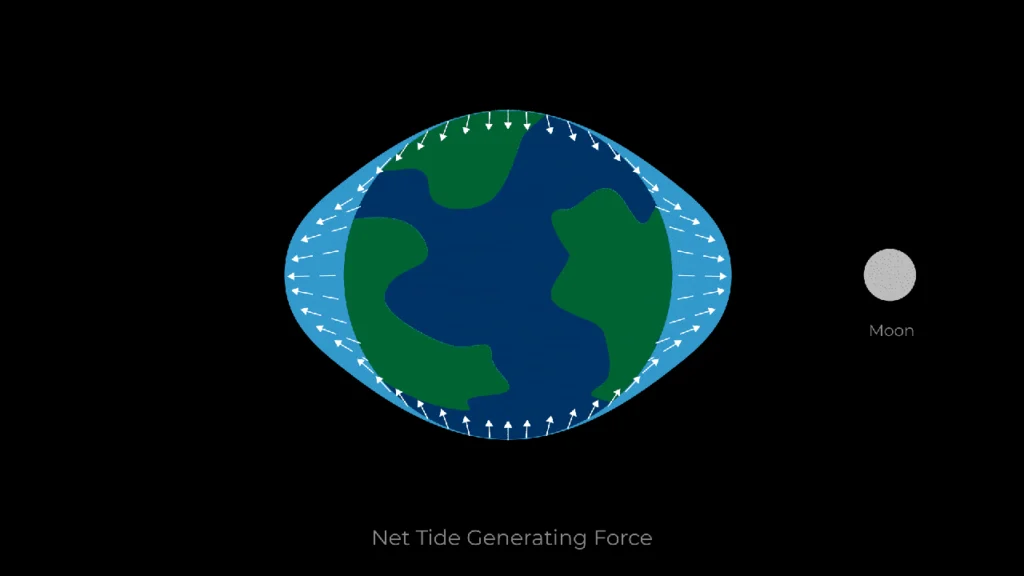
Source: NASA
So centripetal force is one force acting on the oceans, and if it was the only one, there would be no tides, because the centripetal force would be steady and the water would stay where it is. However, the gravity of the Sun and of the Moon also influence the tides. As the Earth rotates, the gravity of the Sun also pulls on the Earth, and on the oceans, causing the water to want to bulge a bit toward the Sun. As the Moon orbits around the Earth, its gravity also pulls the water toward itself. Although it is much smaller and less massive, the Moon is also MUCH closer to Earth than the Sun, so it is the primary driver of the tides. So, we have three major forces pulling on the water of the oceans (actually it pulls on everything including other bodies of water, as well, but tides are generally too small to notice on bodies of water smaller than oceans). When the Sun and the Moon are lined up on the same side of the Earth at the New Moon and Full Moon phases, their gravitational pulls are added together, pulling more on the oceans on that side of the Earth, making for higher tides on that side. There is also still going to be a high tide on the other side of the Earth at the same time (due to the bulge from centripetal force and other factors), but it will be a “lower” high tide than the one on the side toward the Moon. The tides above and below the imaginary line formed by the Sun and the Moon will be low tides, because the water that is making the tides high in one place has to come from somewhere and those places will experience low tide as a result.
As the Moon moves around the Earth and the Earth rotates relative to the Sun, the area on Earth experiencing the greatest combined effect of the gravity of the Moon and the Sun, coupled with the centrifugal force of the rotation of the Earth will be having high tide, and the areas of the Earth 90 degrees above and below that will be at low tide. This is why most places on Earth experience two high tides per day and two low tides. The centrifugal force is always centered at the equator and it is the same everywhere. The Earth is a three-dimensional sphere, so the “bulge” is sort of like a spare tire encircling the globe. The bulge of water it creates would be uniform (highest directly at the equator and lowest at the poles), were it not for the gravitation effects of the Sun and Moon. The tides change due to the Moon and the Sun. As the Moon and Sun change their relative positions, they “pull” on the oceans and, depending on where they are relative to each other and to the plane of rotation of the Earth (the equator), they can make the bulge bigger (like when the Moon is located over the equator) or smaller (like when the Moon is located at a higher latitude). When the Moon is over Canada, for instance, it pulls oceans in that direction, making the bulge from the rotation smaller at the equator, but the water it pulls toward Canada makes the tides high there. When the Sun and Moon are oriented at 90 degrees to one another, their combined gravitational effect on the Earth is at its lowest and there will be lower-than-normal differences between low and high tides, called “neap tides”.

Source: BayofFundy.com
So the tides are generally caused by the gravitational effects of the Moon and the Sun, as well as the bulge caused by centripetal force. There is one other factor which determines how much the tides may change in any particular place, and that is the geography of the shore. The Mediterranean Sea has almost no tides at all, because it is almost completely isolated from the oceans and there is no easy way for the “bulge” of water to move into the Med to create tides. The Bay of Fundy in eastern Canada has the highest tides in the world, with the high and low tides differing by more than 50 feet. There are probably four main factors that contribute to this. The first is the orientation and length of the bay. It is oriented to the southwest, along a curving section of the North American shoreline, so it catches the tidal currents that move along the coast. It is also just the right length so that the movement of the tides in and out of the bay never interfere with each other—the current caused by water flowing out at low tide is gone by the time water starts flowing in with high tide. The Bay of Fundy is also located on the coast of Nova Scotia, and the waters off Nova Scotia are very deep, so there is a lot of water that can move. Relatively shallow basins, like the Gulf of Mexico, generally have lower tides. Finally, the Bay of Fundy is shaped like a funnel, getting narrower and shallower as the tide moves up the bay. This causes the water to sort of “pile up”, creating even higher tides. Check out this web site to see the tide change: http://www.bayoffundy.com/about/highest-tides/#cause .
Isn’t it wonderful how all these things—tides, gravity, force vectors, mass, acceleration, geology, the Moon and everything else are so connected together? That is part of why science literacy is so important. You don’t have to be an expert. You don’t even need to fully understand things. The important thing is that you know enough that you aren’t always depending on someone else to tell you what is going on or why things work the way they work.